In my post on adjusting averages for not-outs in Tests, commenter Rich asked about doing the same in ODI's. At first I thought that this would be too difficult, but I decided that with an hour of mindless copy-pasting from Statsguru, I could at least get it working for individual players.
(Usually I'd rather watch paint dry than copy-paste Statsguru data for an hour, but it's not so bad you're listening to the Champions League football on the radio.)
There's one very important difference for this exercise between ODI's and Tests. In Tests, pretty much all the top batsmen can expect to bat out their innings most of the time. In ODI's, the top order can usually do this, but the middle order often have to slog at the end. So whereas an opener can get a start of 50 and carry on to a century, the number six who gets to 50 will often get out soon afterwards.
So I split the analysis into two parts: one for the top order (1-3), and one for the middle order (4-7). Perhaps 1-4 and 5-7 would have been better, but I can hardly be bothered re-gathering the data.
I only considered batsmen with an average of 35 or more, and only considered innings in the last ten years, since there's been a big explosion in ODI run habits recently.
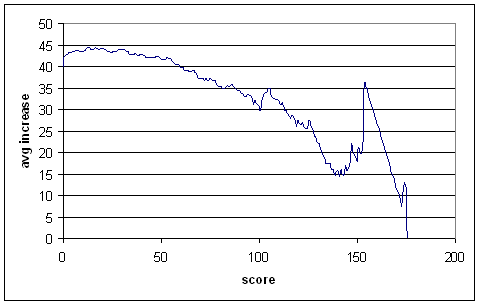
First up, projected increases for the top order:
This is similar to the Test graph — batsmen clearly get their eye in after scoring some runs — but the downward trend starts much earlier, as is expected. After about 60 runs, the average increases are less than the overall average for this dataset (almost exactly 40). So not-outs tend to deflate averages when the score is below 60, but inflates them afterwards.
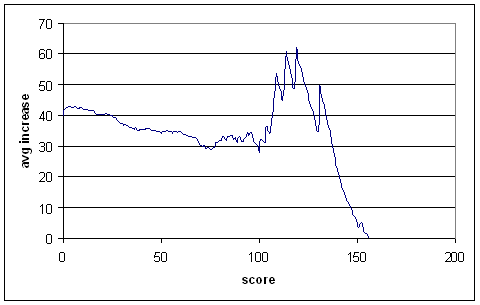
And now for the middle order:
I wouldn't pay much attention to the curve out past 100, since there's not much data there. It won't make too much difference, since there aren't that many unbeaten centuries in the middle order.
The curve is quite different from that of the top order, in roughly the way we would expect. Not-outs have a deflating effect on averages only up to 25 runs or so, and after that they inflate averages.
Now, I haven't done a thorough analysis on all batsmen, since I don't have that data handy. I've just done some selected cases. Some caveats: Some of the batsmen played earlier than ten years ago, and perhaps the average increase curves was different then. Also, I've applied either top order or middle order adjustments to each batsman, and not both. This won't have too much of an effect, but to do it properly you'd want to split the innings into top-order and middle-order and do them separately. If a batsman's highest score was a not-out, I added the average increase to it. (For Tests, I added the batsman's regular average, but doing so in ODI's is much less accurate.)
In the table below there are four averages presented: the regular average, one adjusted based purely on the batsman's own scores, one based purely on the relevant graph above (shifted up or down to match the batsman's regular average), and one mixture of the two, giving more weight to the graph when the batsman doesn't have many scores greater than or equal to the not-out being projected. I've called these reg, ind, gph, mix. The latter one is the one I'd go with. There's two openers, and the rest from the middle order.
player inns no reg ind gph mix
SR Tendulkar 407 38 44,3 43,4 43,9 43,5
SC Ganguly 300 23 41,0 40,6 40,6 40,6
---
MG Bevan 196 67 53,6 48,1 52,4 48,8
L Klusener 137 50 41,1 41,7 40,1 41,4
MEK Hussey 64 26 55,6 55,0 54,4 54,9
A Symonds 154 32 39,7 40,1 39,0 39,9
DR Martyn 182 51 40,8 42,1 40,0 41,6
RP Arnold 155 43 35,3 33,5 34,6 33,8
Bevan's average has, contrary to my expectations, been pulled back quite a bit, down below 49. Nevertheless, it's still a lot higher than most Bevan sceptics would have it. I wouldn't want to draw too many general conclusions from what was a deliberately biased set of batsmen (all with fairly high not-out proportions), but it looks like ODI averages can be and sometimes are inflated by not-outs much more than Test averages.