Schrodinger’s Bat – Rating Unidentified Players
Dave Wilson |
I’ve been banging on now for about two years, extolling the virtues of match impact as a more enlightening measure of a cricketer’s value than traditional averages. Match impact is based on comparing the team’s win probability before and after an event such as a batting partnership or the fall of a wicket, and apportioning the responsibility for those changes in win probability, both positive and negative, to the players involved. Those of you who stayed with me this far may be interested to know that I’m almost done rating all players from Zaheer Abbas to Agha Zahid and all points in between.
DESIGNING THE SYSTEM
Information Gathering
The first thing to do was to fashion a database of the batting partnerships and fall of wickets for all Tests played to date; considering that there could be a maximum of ten partnerships plus ten dismissals for each innings, this was potentially 80 events per Test for 2,000+ Tests or 172,000+ database entries (actually it worked out at around 68 events per Test, not even 150,000 entries – a mere bagatelle). At that point I could assess how many Tests had enjoyed the same match status as the match which was being assessed and also their outcomes, and hence determine the win probability at that point in the match, both before and after the event.
For example, a team is chasing a target of 250 and sit at 39/4, at which point two batsmen share in a partnership of 100, at which point one is dismissed, caught behind; the change in win probability of the batting team from the beginning of the partnership to its conclusion results in an increase of for the batting team of about 26%, while the fall of the wicket results in a decrease of 23%, which is conversely an increase for the fielding team. The out batsman receives a positive share of the increase in win probability due to the partnership (and any previous partnerships in which he was involved), and a negative share of the decrease in win probability as a result of his dismissal. The bowler and wicket-keeper receive a positive share of the change in the fielding team’s win probability as a result of the dismissal.
I always strive to keep any investigations I carry out completely objective, which can be difficult. The reason I try to do this is because, once subjectivity is involved, there’s a tendency to try and “fix” the outcome if player A is either rated too high or too low. The first decision in that regard for match impact was in the apportioning of win probability deltas between bowlers and fielders (ffor dismissals where fielders are involved). To be perfectly objective, a 50/50 share must be used between bowlers and fielders; any other division brings in subjectivity. What would be correct – 40/60? 75/25? It’s impossible to say for sure, so 50/50 was decided upon. The benefit of an even split is that wicket-keepers, who typically don’t bowl, are not forced way down the list by an unequal, subjectively weighted split.
Another decision involved the assessment of changing run rates; a team chasing 250 has a different win probability if the batting team is Australia in 2004 than if it’s South Africa in 1892. The ICC Test team ratings system stipulates that a one-sided contest occurs when the differential in ratings between the two teams is 40 or more, so that qualification can also be used here. The era can also be incorporated into the assessment, however there is a point beyond which the results generated are based on a sample size which is too small to be reliably informative.
And what about draws – should a player be rewarded for his part in achieving a draw? How do we determine at which point the player has decided his team can’t win and changed his goal to ensuring his team doesn’t lose? Does that change between different eras? Is it different for different players? Those decisions seem completely subjective to me as well as being impossible to determine. In the end though, because of the way this measure is designed the actual match outcome is immaterial (unless the event being assessed ends the match), as the win probability at the time is used to determine the player’s impact, not the final result.
Assessing the Results
So the database was used to generate every Test player’s impact for his batting, fielding and bowling performances for each Test in which he played, giving a match impact rating for every match and ultimately his career. As the rating is a single value which incorporates all discplines, it allows us to rate all players together, on a level playing field as it were, without having to separate out batsmen, bowlers etc. Though of course that can be done as well – the rating is based solely on impact, so bowlers could for example be rated on bowling only, or all impact including batting and fielding too; personally I prefer to rate players based on all disciplines, as that assesses their impact completely – in other words they should be considered based on their total contribution. This gives us a reasonable basis to compare the exloits of an allrounder as against those of a top batsman or fast bowler, as the measure is based solely on the impact the player’s performance has on the likely outcome of the match.
So the decision to be made at the point where we had career match impact numbers for all Test players was how to assess the results – should we rate players on the total impact over their entire career, or the average impact per Test? What about his highest match impact? Perhaps more information could be gleaned from plotting the impact numbers for each player for all Tests? A profile was then produced for players which displayed their peaks and troughs over their career, revealing details which a simple total or average can’t do.
Looking at profiles where the impact values are plotted for each Test was uninformative as they are too variable, such that no trends can be discerned; similarly averaging over a period of ten Tests wasn’t particularly informative either, as there was then not enough variation. Averaging over five Tests proved to be the key, being a) variable enough to highlight the player’s individual career peaks and troughs and b) having a certain resonance in relation to the five-Test series, which was the norm for many years. So I plumped for a moving average over five Tests.
After looking at the profiles of each Test cricketer over a long period, I was able to develop a feel for what the level of greatness was as regards match impact average. Basically, a 5-Test average of 20% match impact is about the hallmark of true Test class – this doesn’t mean a career average of 20%, hardly anyone maintains that over a complete career, rather the higher quality players achieve a peak of over 20% at one or more points of their careers. Indeed, the greats achieve a peak of 30% over a five-Test average, while the all-time greats reach 40%. A very small number have attained a 5-Test average of over 50% – indeed, you can count them on the fingers of one hand.
We can also rate players on the number of Tests their moving average was maintained over that 20% mark, or indeed the area under the curve formed by their profile and the 20% line. Or we can count the number of matches in which they achieved a certain impact level (say 30% or 40%), though as I’m trying to rate players over their careers that’s of more interest at the match level.
RATING THE PLAYERS
So finally we have a great deal of data which we need to make sense of. To illustrate what I’m trying to do here, and to show the difference bwtween comparing players based on match impact as compared to traditional averages, consider Graham Gooch and David Gower – similar number of Tests player (118 vs 117), Gooch with a small advantage in runs scored (8900 vs 8231), while Gower has the upper hand in terms of average (42.58 vs 44.25). The graphic below shows their career match impact profiles:-
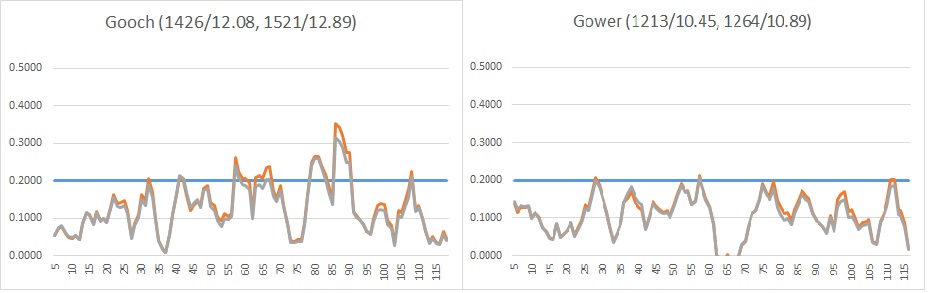
Click to enlarge.
The grey line represents raw data and the orange is adjusted as described later in this article; numbers in parentheses show Raw Total Impact, Raw Average Impact, Adjusted Total Impact and Adjusted Average Impact.
We can see that their aggregate and average impact is not hugely different, however reviewing the the profiles and using the 20% (or 0.2, shown in blue) threshold as a guide, shows that though both have enjoyed ups and downs, Gooch has had far more impact that Gower. But how can we capture that in a single rating?
We have different ways of measuring player impact, e.g. total, average, peak, duration over 20%, area under the curve formed with the 20% line, etc. – how to assess these parameters that have levels which sit at different magnitudes without swamping the smaller values? In researching the most appropriate method of summarising these various parameters in a single measure, it became apparent that the answer was to use the geometric mean, which uses the product of the values, rather than the sum as the arithmetic mean does.
Schrodinger’s Bat?
When I first make my assessments of a ranking or rating system, I strip off the identifying aspects of the players (name and nationality) and just leave a player ID number for later cross-reference. I leave in their main discipline (batsman, bowler, all-rounder, wicket-keeper) and era in order to be able to check for system bias, and also avoiding bias of my own as I can’t easily recognise which player is which . Once the (unidentified) players are ranked we don’t know which player is number one – it may be Bradman, it may be Sobers, it may even be Tendulkar, but until we apply the cross-reference of player IDs to player names, it could be any of them, or none, sort of a Schrodinger’s Cat situation.
Anyway, looking at the geometric mean of the raw data only, when we rank the players what we find is that the top 50 is made up of 20 all-rounders, three wicket-keepers, 18 bowlers but only nine batsmen – at this point I don’t know which players are represented. Is that correct? Well, that’s what the raw numbers are telling us, that there are twice as many bowlers who have been all-time greats than have batsmen, which some will agree with, though others won’t. I would personally be OK with that, as it may be that by using a method to rate players on everything they do we have unearthed the fact that bowlers contribute more – after all, they bowl, field and bat which most others don’t.
If we look a little closer though, we find that of the 18 bowlers, six are players who plied their trade around the turn of the century (19th to 20th, that is). Now, it may be that this is the case, i.e. six of the best 18 most impactful bowlers of all time played in the 19th century, however this suggests that a third of those top bowlers all played in the first 130 or so Tests, and the next 2000-plus Tests only produced another 12 who were as good – I personally doubt that is the case, and this may be the kind of system bias I am seeking to avoid, so let’s delve deeper.
This is how it looks for all eras as regards raw data and numbers of players in the top 50:-
| Era | #Tests | Debuts | Raw | % |
| Pre-WW1 | 134 | 372 | 10 | 2.68% |
| Inter-war | 135 | 360 | 5 | 1.39% |
| 40s/50s | 215 | 388 | 4 | 1.03% |
| 60s/70s | 384 | 439 | 8 | 1.82% |
| 80s/90s | 611 | 629 | 15 | 2.38% |
| 2000s | 679 | 595 | 8 | 1.34% |
Clearly the pre-WW1 years are over-represented, and as mentioned above this is mainly because of the presence of a number of early era bowlers. The 1980s and 1990s are more heavily represented than the 2000s, in fact more than twice as many based on percentage. Personally I think this may be because we enjoyed a golden age of cricket during that period as compared to the post-milennium era – certainly the august members of the ICC Hall of Fame voting committee agree, as there are almost twice as many inductees from that period than any other.
Get to the point, Dave
So at last we come to the point of the subject matter – should raw data be used to assess players, or should we adjust for issues such as era and strength of opposition? Closer investigation reveals that other factors are at work in shoving the old-time bowlers to the top of the tree, namely the changes over time which have resulted in far fewer unassisted dismissals for bowlers (i.e. bowled, lbw), as well as the changing division of labour as regards bowlers – turn of the century opening bowlers had a far higher share of the overs than is common nowadays. In the 19th century opening bowlers enjoyed 60% of the bowling, whereas modern bowlers average around 40%, and this can be adjusted for.
As regards the issue of opposition strength, George Lohmann is a prime example of the importance of this aspect. As I showed in an earlier piece, Lohmann’s eye-opening average is largely a result of taking a hatful of South African wickets when they were decidely minnows, and once again the ICC comes to the rescue, or at least the extended ICC ratings which I developed – the raw data can be adjusted based on the strength of the opposition as compared to the average.
Finally, we have to address the issue of players who produced impactful performances but who appeared in a small number of Tests – how do we compare Ranji’s 15 Tests with someone like Steve Waugh? This should also be factored in.
Applying the above adjustments gives us a modified rating (as opposed to that based on raw unadjusted data), and if we re-rank and examine the revised top 50 we see that we now have 18 all-rounders, four wicket-keepers, 14 bowlers and 14 batsmen – clearly a much more balanced representation of the various disciplines. But is it right? Certainly we now have only two early era bowlers as opposed to six.
We can also look at the make-up of the list based on era – here are the before and after numbers based on era:-
| Era | #Tests | Debuts | Adj | % |
| Pre-WW1 | 134 | 372 | 4 | 1.08% |
| Inter-war | 135 | 360 | 3 | 0.83% |
| 40s/50s | 215 | 388 | 4 | 1.03% |
| 60s/70s | 384 | 439 | 9 | 2.05% |
| 80s/90s | 611 | 629 | 19 | 3.02% |
| 2000s | 679 | 595 | 11 | 1.85% |
I’ve deliberately avoided identifying the highest ranking players as it provokes a subjective assessment of whether or not their inclusion is justified or not. I have a few players still left to assess, at which point I’ll post the findings.
CRITIQUE OF OTHER RATING SYSTEMS
All of the other systems of which I’m aware rate players or performances separately by discipline, except Impact Index, though the level of subjectivity involved in that measure is significant. The more aspects which are taken into account, though it makes the system appear more complete, the necessary weighting involved makes the results even more subjective, and that doesn’t change regardless of the degree of acceptance amongst the cognoscenti. How much you’re prepared to believe in a subjectively weighted system depends largely on whether or not the final list agrees with your own opinion.
And therein lies the danger of subjectively weighted ratings. There is a natural tendency to “fix” the ratings if they don’t “look right”, by which I mean if it seems that some players are ranked too high and some too low as compared to the ratings developer’s own opinions or those of received wisdom. Once we start fiddling with the weightings to right those wrongs, we may as well just rate totally subjectively by personal opinion, as with a subjectively weighted system you can never know for sure if it’s correct.
The Wisden 100 individual performance ratings, which are objective insofar as they are based solely on information on the scorecard, nonetheless also suffer as a result of not directly measuring impact. To make the match impact rating totally objective, we would look at the raw data only, which is why I show both raw and adjusted data in the profiles above.
With match impact, however, we have a system which is objective, being based solely on the change in win probability as a result of a particular individual performance, as well as being impartial as regards discipline, i.e. batting, fielding or bowling. That allows us to objectively rate, and rank, all players based on all aspects of their performance which impact the result.
Schrodinger’s Cat remains potentially alive. For now.





Leave a comment