On quite a number of occasions it has been that the umpire's decision to award a potential snick behind has been series-defining. Pakistan suffered a series loss as a result of Jimmy Adams being given not-out by a heavily biased Billy Doctrove in the Antigua Test of 2000, and the same fate befell Pakistan after Umpire Porky Parker's decision not to dismiss Langer in the 4th innings of the 1999 Hobart Test.
Given the problems with the snickometer and even larger inconsistencies with Hotspot, I was thinking at how the current system could be improved. I believe I've come up with a relatively simple answer.
Unlike LBWs and their "≥ 50% of the bowl needs to be striking the stumps to be given out" ruling because of possible deviation after rapping a batsman on the pads, a snick has to go through to the keeper by definition.
Let's suppose a batsman feathers through the ball to the keeper whilst simultaneously striking the bat - or being infinitesimally close to striking it - on the ground. Now that rules out any decisions made on the basis of the sound, or at the very least brings it subjectivity into the equation (whether there was a "wood"). So really the only things you can rely on is either Hotspot - which has proved itself that it can not be relied upon - or the deflection. But what if there's no discernible deviation from the perspective of the eye?
Here's where my pretty rudimentary solution comes in. Let me just apologise in advance for the oncoming mathematical jargon. I'll try to keep it short and sweet.
For ease of understanding, I will clarify a few terms before beginning:
Normal - an imaginary line that runs from the batting/popping crease to the wicket-keeper.
Parabola - just a term for a symmetrical curve (x^2 on a graph) or for people who despise all things maths, a symmetrical hill for example.
Horizontal (in this scenario) - any imaginary line that is parallel to the popping crease.
Vertical (in this scenario) - any imaginary line that is upwards from the ground, i.e perpendicular to the pitch.
Velocity - speed in a particular direction.
Now that I've tried to define the terms used, here's my explanation of exactly what I mean.
We know from physics principles that a ball travelling with a horizontal and vertical velocity (speed with direction) will roughly travel in a parabola because of gravity (curve from when it is released to when it strikes the ground). So a ball which pitches on the wicket arrives into the keeper's gloves after having a curve-like trajectory (picture below). Drag, air resistance and the Magnus Effect also alter the trajectory but they can be accounted for in a computerised model. Thus I am ignoring them and assuming that only gravity and air resistance/drag force (which mainly varies the speed of the ball, which I am not going to discuss) affects the ball for simplicity.

Now, even the most marginal of edges will affect both the speed of the ball (more difficult to detect possibly, considering the high precision equipment that would undoubtedly be required) and its direction. It's the latter I'm most interested in.
Consider Hawkeye with a line running through the centre of the ball (a tangent of its position in its trajectory at any instant - a tangent being a straight line with the same gradient as the curve/parabola at a particular point on the parabola). Given edges are usually from the side of the bat, I'd hunch a bet that even the deftest of edges incurs a slight horizontal right-to-left, or vice-versa, deflection (looking through the bowler's eye and in the frame where the bowler's height/upwards from the ground is deemed to be the perpendicular vertical z-axis), even if not distinguishable to the naked eye.
Utilising Hawkeye, the ball will continue along its expected trajectory (at least in the horizontal x-direction) instantly after passing the bat, unless it has induced the edge. In which case the trajectory will have been altered due to the impact force of the bat on the ball. The slope but more importantly the angular direction from the normal of the line (term defined above) running through the ball will therefore no longer correspond to the predicted trajectory. The angular direction is the angle between the line running through the ball (the tangent) and the normal line - in the horizontal x-axis frame.
A (very!) crude and unartistic image explanation of this is below. Assume the batsman strikes the ball directly above the batting/popping crease in the edged ball scenario.
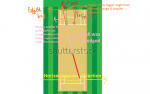
Any concerns arising about changes to the ball's trajectory due to the ball swinging/deviating after passing the stumps can invariably be dismissed. We are only wanting to find the predicted trajectory instantaneously after passing/potentially striking the bat. In 999/1000 cases differences in trajectory just before passing the bat and just after passing the bat will be due to the parabolic effect of trajectory. Other effects such as swing are negligible.
Thus, this computerised predicted trajectory derived from Hawkeye will be almost identical to the trajectory of the ball just before passing the bat (assuming there was no edge), save for minor differences due to the parabolic effect that gravity causes to objects with both a horizontal and vertical trajectory.
To conclude the mix-tape of information above, basically an edge will cause a variation in trajectory from what is expected and any possible variation can be determined by considering if the actual trajectory of the ball (in particular its angular direction from possible impact to the wicket-keeper) matches that of the predicted trajectory produced by a computer. If it doesn't then clearly in 99.9% of cases an edge will have caused the deflection and the batsman should be given out.
Therefore, no more of the nonsensical judging deflections on eye alone and commentators claiming "that sounded wooden".
Combined with the snickometer I think this will be very good technology for the ICC to implement. The principle of Hotspot is far too technical when you factor in the range of factors that affect it and consequentially its inaccuracy, whereas this is quite a simple principle based on a number of fundamental physics principles (Newton's 1st Law of Motion and conservation of momentum).
[I hope I explained myself well enough. It's late here and my brain may not be functioning properly at this time.]
What do you guys think about this idea?
Given the problems with the snickometer and even larger inconsistencies with Hotspot, I was thinking at how the current system could be improved. I believe I've come up with a relatively simple answer.
Unlike LBWs and their "≥ 50% of the bowl needs to be striking the stumps to be given out" ruling because of possible deviation after rapping a batsman on the pads, a snick has to go through to the keeper by definition.
Let's suppose a batsman feathers through the ball to the keeper whilst simultaneously striking the bat - or being infinitesimally close to striking it - on the ground. Now that rules out any decisions made on the basis of the sound, or at the very least brings it subjectivity into the equation (whether there was a "wood"). So really the only things you can rely on is either Hotspot - which has proved itself that it can not be relied upon - or the deflection. But what if there's no discernible deviation from the perspective of the eye?
Here's where my pretty rudimentary solution comes in. Let me just apologise in advance for the oncoming mathematical jargon. I'll try to keep it short and sweet.
For ease of understanding, I will clarify a few terms before beginning:
Normal - an imaginary line that runs from the batting/popping crease to the wicket-keeper.
Parabola - just a term for a symmetrical curve (x^2 on a graph) or for people who despise all things maths, a symmetrical hill for example.
Horizontal (in this scenario) - any imaginary line that is parallel to the popping crease.
Vertical (in this scenario) - any imaginary line that is upwards from the ground, i.e perpendicular to the pitch.
Velocity - speed in a particular direction.
Now that I've tried to define the terms used, here's my explanation of exactly what I mean.
We know from physics principles that a ball travelling with a horizontal and vertical velocity (speed with direction) will roughly travel in a parabola because of gravity (curve from when it is released to when it strikes the ground). So a ball which pitches on the wicket arrives into the keeper's gloves after having a curve-like trajectory (picture below). Drag, air resistance and the Magnus Effect also alter the trajectory but they can be accounted for in a computerised model. Thus I am ignoring them and assuming that only gravity and air resistance/drag force (which mainly varies the speed of the ball, which I am not going to discuss) affects the ball for simplicity.

Now, even the most marginal of edges will affect both the speed of the ball (more difficult to detect possibly, considering the high precision equipment that would undoubtedly be required) and its direction. It's the latter I'm most interested in.
Consider Hawkeye with a line running through the centre of the ball (a tangent of its position in its trajectory at any instant - a tangent being a straight line with the same gradient as the curve/parabola at a particular point on the parabola). Given edges are usually from the side of the bat, I'd hunch a bet that even the deftest of edges incurs a slight horizontal right-to-left, or vice-versa, deflection (looking through the bowler's eye and in the frame where the bowler's height/upwards from the ground is deemed to be the perpendicular vertical z-axis), even if not distinguishable to the naked eye.
Utilising Hawkeye, the ball will continue along its expected trajectory (at least in the horizontal x-direction) instantly after passing the bat, unless it has induced the edge. In which case the trajectory will have been altered due to the impact force of the bat on the ball. The slope but more importantly the angular direction from the normal of the line (term defined above) running through the ball will therefore no longer correspond to the predicted trajectory. The angular direction is the angle between the line running through the ball (the tangent) and the normal line - in the horizontal x-axis frame.
A (very!) crude and unartistic image explanation of this is below. Assume the batsman strikes the ball directly above the batting/popping crease in the edged ball scenario.

Any concerns arising about changes to the ball's trajectory due to the ball swinging/deviating after passing the stumps can invariably be dismissed. We are only wanting to find the predicted trajectory instantaneously after passing/potentially striking the bat. In 999/1000 cases differences in trajectory just before passing the bat and just after passing the bat will be due to the parabolic effect of trajectory. Other effects such as swing are negligible.
Thus, this computerised predicted trajectory derived from Hawkeye will be almost identical to the trajectory of the ball just before passing the bat (assuming there was no edge), save for minor differences due to the parabolic effect that gravity causes to objects with both a horizontal and vertical trajectory.
To conclude the mix-tape of information above, basically an edge will cause a variation in trajectory from what is expected and any possible variation can be determined by considering if the actual trajectory of the ball (in particular its angular direction from possible impact to the wicket-keeper) matches that of the predicted trajectory produced by a computer. If it doesn't then clearly in 99.9% of cases an edge will have caused the deflection and the batsman should be given out.
Therefore, no more of the nonsensical judging deflections on eye alone and commentators claiming "that sounded wooden".
Combined with the snickometer I think this will be very good technology for the ICC to implement. The principle of Hotspot is far too technical when you factor in the range of factors that affect it and consequentially its inaccuracy, whereas this is quite a simple principle based on a number of fundamental physics principles (Newton's 1st Law of Motion and conservation of momentum).
[I hope I explained myself well enough. It's late here and my brain may not be functioning properly at this time.]
What do you guys think about this idea?

